Music
Theory Fundamentals
Part I –Pitch & Standard Notation
This booklet is intended to be a ‘crash course’ in the fundamentals of music theory. In order to fully explain every element this booklet would be hundreds of pages long, and besides, there are countless great authors who have done just that! The aim of this booklet is to cover the basics and allow the reader to use it as a foundation of knowledge to build upon.
In order to effectively understand and communicate music it is important to become familiar with the fundamentals of standard notation. Although there are other systems of notation (guitar tablature for example), standard notation is by far the most popular and is used all around the world. This system is shared by most tonal instruments and it acts as a common language, making communication and understanding simple. Even if you don’t frequently use standard notation and play primarily by ear, these concepts will help you understand music theory on a deeper level just as understanding the written word helps with language in general.
The three primary elements of this system (and of music in general) are; rhythm, pitch and harmony. We will start by examining pitch in more detail.
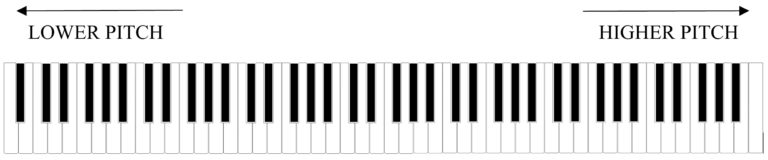
In music, the term pitch refers to the relative ‘highness’ or ‘lowness’ of a sound. Specific pitches are named by using the first seven letters of the alphabet: A B C D E F and G. We tend speak of pitch as a specific tone that is placed and notated. We use a musical ‘stave’ to organize these tones.
A brief scientific definition
Although musicians do not primarily think of and address pitches as frequencies but rather as notes, it is still useful to understand the very basics of the underlying physics of sound.
A ‘sound’ is a vibration that propagates through air (or any other medium) as an acoustic wave. The speed of the vibration is known as frequency, and this determines the pitch of the sound. Frequency is measured as the number of wave cycles that occur in one second. The higher the frequency, the higher the pitch.
The unit of frequency measurement is Hertz (Hz for short). A frequency of 1Hz means one wave cycle per second. When we think about the note ‘A’ we expect to hear a sound wave that oscillates 440 times per second. An ‘A’ an octave higher would be double the frequency (880Hz) and an ‘A’ an octave lower would be half the frequency (220Hz).
The Stave
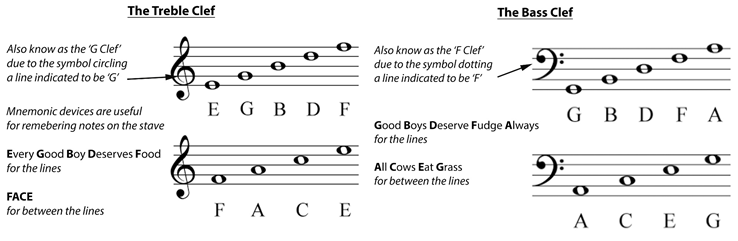
The stave (or ‘staff’) is written using 5 horizontal lines. Notes are placed on or between these lines representing a specific note. These notes can also be placed outside of these five lines when a pitch is too high or too low. We call these ledger lines. They help extend the range of the stave. In addition to the stave we also have clefs. These symbols indicate the exact pitch of the written notes. When placed on a stave, it indicates the name and pitch of the notes and acts as a reference point. The most common clefs are the treble (or ‘G clef’) and bass (or ‘F clef’). Although there are more we will be focusing on these primarily. This information is more easily understood using the diagrams below.
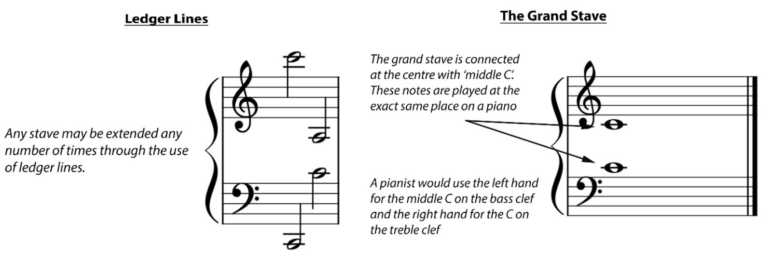
The Grand Stave is made up of both the treble and bass clef. Piano music in particular is notated using this stave as it covers a wide pitch range and allows for a simple approach where the left hand plays the lower bass clef and the right hand plays the higher treble clef. This stave is connected in the middle with an invisible ‘middle C’ that can be notated on either clef.
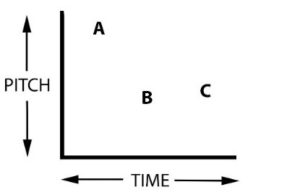
It can be helpful to think of the stave as an X/Y axis graph. Pitch being the vertical, up and down Y axis and ‘time’ being the horizontal, rhythmic X axis. In the diagram below, A is the highest pitch and occurs first in time. B is the lowest pitch and occurs after A but before C, which is slightly higher in pitch. Standard notation works using the same basic principles.
The Octave
As mentioned previously, we use the letters A B C D E F and G to organize pitch. If we continue past G we go up to A and the pattern repeats itself. We call the distance between these two A’s an octave.
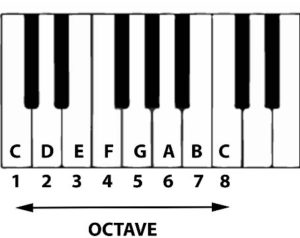
Musical instruments often have a number of different octaves in their range. The 88-key piano for example has 7 full octaves known octave registers. This system allows us to specify the exact register of a note. ‘Middle C’ is known as C4, a very useful reference point in music. The note immediately to the right of C4 is D4, and the note immediately to the left is B3.
Sharp, Flat and Natural
The 7 notes discussed so far (A to G) are also known as natural notes. There are also another 5 notes that are known as sharps (#) or flats (b). The natural notes are represented on a keyboard with white keys and the sharp/flat notes are represented by black keys.
We now have 12 separate pitches but only 7 letters. In order to specify these new notes we use the terms sharp and flat. We also have a set of symbols that can be placed before notes on a piece of music. Here are the three most commonly used symbols:
Sharp – # Flat – b Natural – ♮
In the diagram below we see the symbols used in context. The first note is a D flat, the second is a D (natural) and the third is A sharp
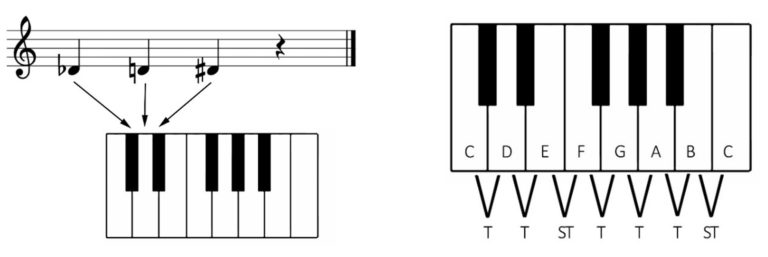
A ‘sharp note’ is assumed to be one semitone higher in pitch than the natural note and a ‘flat note’ is assumed to be one semitone lower than the natural. We can also look at these notes in different ways. The note G# is exactly the same sounding note as Ab; we call these enharmonic notes.
The semitone (also known as a half step) is the smallest difference in pitch that we acknowledge in Western music. It is the distance from a key on the piano to the very next key, white or black. On a guitar this would be an adjacent fret.
The whole tone (or whole step) is a distance of two semitones. For example, on a keyboard the distance between a C and a D is a whole tone.
The Major Scale
The Major scale is a specific pattern of semitones and whole tones within an octave. It is the foundation of western tonal music and serves as the basis of music theory. We will start off by looking at C Major.
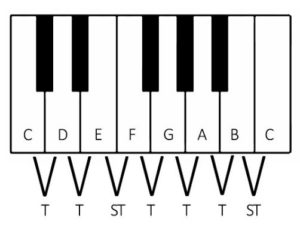
As you can see in the diagram above, the C Major scale only uses the 7 natural notes with no sharps or flats. As with any Major scale, we apply a specific pattern of tones and semitones when we start from any given note. If we were to construct a Major scale starting on a D instead of a C we would come up with a different set of notes: D E F# G A B C# (D).
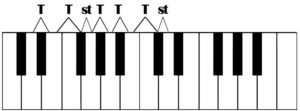
All scales that we use in music can be looked at as a specific pattern of notes. This pattern would apply regardless of the starting tone. It is important to learn the structure of the major scale as we constantly refer to it as a reference point. This will be explained further in this booklet.
Keys & Key Signatures
A Key is simply the major or minor scale that a piece of music uses. You will hear terms like “this song is in the key of D Major”. This means that the song will primarily use the notes that make up the key of D major and the note D in particular would act as the “home” note, knows as the root note or tonic.
We have 12 major keys and 12 minor keys. Each Major key has a minor key that is directly related to it and uses the exact same notes but a different starting point (root note). These minor keys are generally perceived to be being ‘sad’ sounding and have a darker quality in contrast with the major scale.
The term key signature specifically relates to standard notation and the stave.
Imagine we are in the key of C, the simplest of all keys with no altered notes that are sharp or flat. The notes of the stave would be easy to read and follow.
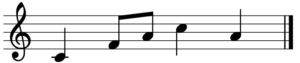
Now imagine we are in the key of B, which has 5 sharps. This is tougher to read as you have to think about individual notes and make sure you alter the correct one.
In order to make this process simpler we use a key signature which is placed at the beginning of a piece just after the clef. In this case the five sharp symbols tell the player the piece is in B major. Notice that they are placed on the actual notes on the stave that they represent.
This makes the piece easier to read as there is less visual information to process!
Part II – Rhythm
This part of the booklet will focus on rhythm; the time aspect of music. Unlike a painting or a sculpture, which are compositions in space, a piece of music is a composition dependent upon time. Rhythm is music’s pattern in time.
Time is accounted for in standard notation in the form of notes and rests (empty space). These two elements together fill out a bar of music and allow us to visually understand and be able to apply very specific rhythms.
Duration
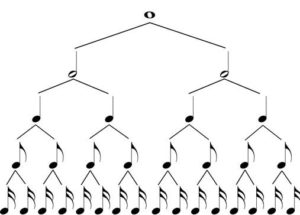
In music, duration is the amount of time in which a note is played (or a rest). We use a system of symbols that represent specific note durations as shown below:

Although the above diagram covers the foundational rhythm durations, we also have other symbols to represent other alterations.
We use ties and dotted notes to extend note duration while trying to keep it as simple as possible to understand both visually and intellectually. A tie is a curved line that connects two notes of the same pitch creating a longer continuous note. A dotted note is a dot placed after a note indicating that it will be extended an extra one-half of its original value.
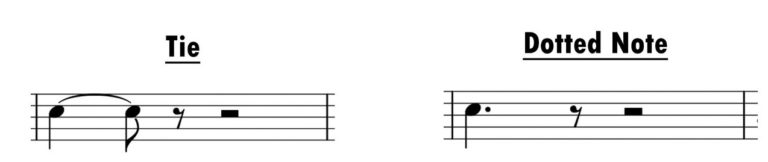
The examples shown above have the exact same overall rhythmic and will sound identical to the listener; they are simply presented in a different way. Below we see examples of how certain beat values are equivalent to others.

Beat Value and Tempo
The beat is the basic pulse of a piece of music. It is the steady rhythm that you would tap your feet or nod your head to. The speed of that pulse is known as tempo. There are two primary ways in which we specify a particular tempo. One method is the use of traditional terminology like adagio and presto for example. Each of these terms represent a generally agreed upon tempo.
We can also use specific measurements with the term bpm. This shows the exact number of beats that would occur in one minute. If a piece of music was to be played at 60 bpm that would mean that one beat would occur every second and 60 would occur every minute. We also specify the note value of every beat as shown below:
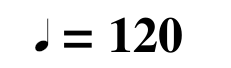
This tells us that the piece is to be played at 120 beats per minute with every beat being represented by a quarter note.
Meter & Time Signature
Beats tend to be grouped into specific patterns. The most commons patterns are groups of 2, 3 and 4. These rhythmic patterns allow us to construct measures or bars in standard notation. This system of bars allows information to be broken down and understood in manageable chunks.
In music such grouping is achieved by actual stress—i.e., by periodically making one note stronger than the others. When the stress occurs at regular intervals, the beats fall into natural time measures.
A time signature is a symbol with 2 numbers, one on top of the other, at the beginning of the stave that tells the musician how many beats occur in each bar. The top number tells us how many beats are in the bar and the bottom number tells us what note value the beat represents.
In the example below we have 4 quarter note beats per bar

A listener can usually tell what the top number of a time signature is likely to be without seeing the music because there is usually a natural pattern of strong and weak beats. The bottom number is more specific to standard notation and reading. In the diagram above you will notice that some notes are connected by horizontal lines that we call beams. These beams help us see notes that occur with a beat. The two quarter notes in this example are not ‘beamed’ to any others as they already represent an entire beat. The single line beam represents connected eighth notes and the double beam represents connected sixteenth notes. Beams allow a musician to instantly identify where each beat in the bar occurs and this results in a simpler reading system.
Part III – Harmony
This part of the booklet will focus on harmony; a simultaneous sounding of notes.
We will begin by studying intervals; the measurement of distance in pitch between two notes. Intervals are the building blocks that, when combined in certain patterns, form chords. We will be using the major scale as a tool to understand the basics of intervals. It should be noted that intervals can be heard and perceived both melodically (played one after another) and harmonically (played at the same time).
We use a system of counting scale degrees. When we reference, for example “the 4th degree of the Major scale” we are talking about the 4th note in the major scale sequence. Each of these notes have a unique distance to the root note and has a very particular sound quality.

Although there are 12 intervals contained within an octave, learning the Major scale well is a great way to start learning these intervals both by ear and visually on your instrument.
We also use also use some extra terminology called modifiers to further explain the type and characteristic quality of an interval.
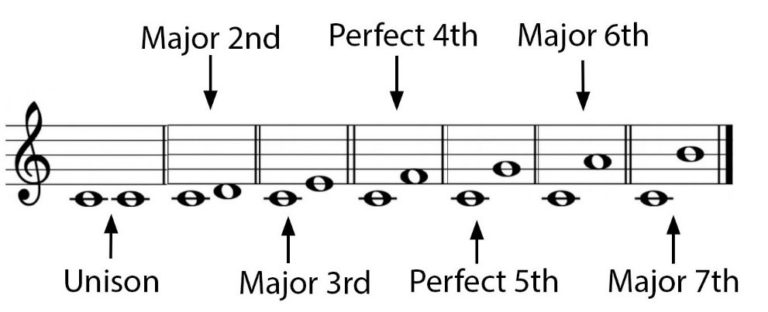
Major, minor, augmented, diminished and perfect. Let us begin by looking at the 12 intervals contained within an octave

The major and minor modifiers are used to characterize the 2nd, 3rd, 6th and 7th degrees. These intervals often hold the sound quality that determines whether a chord is major or minor in tonality. The Major scale for example only uses Major intervals and no minors
The perfect modifiers are used with 4ths and 5ths, unisons and octaves. These intervals are stable and don’t imply any major/minor tonality.
The augmented and diminished modifiers are used primarily to describe the 4th and 5th degrees that have been altered. To ‘augment’ means to increase the size of an interval while to ‘diminish’ means to reduce the size of an interval. An augmented 4th simply means that the 4th interval has increased in size by a semitone. A diminished 5th simply means that the 4th interval has increased in size by a semitone. The term tritone is also commonly used to describe the augmented 4th/ diminished 5th. Below we see the intervals used within the Major scale (octave not included in the diagram). Minor scales, blues scales, pentatonic scales etc. are all built using different combinations of these 12 fundamental intervals.
Consonance vs Dissonance
Some harmonic intervals are considered to be consonant (pleasing) to the ear ans some are considered to be dissonant (tense) to the ear. In generic terms we often consider major intervals to be “happy” and minor intervals to be “sad”. Due to the wide array of different tonal characteristics, it can perhaps be easier to think of chords, scales and intervals as being on a scale between brightness and darkness.
Harmonic movement in music can be perceived as tension and release. Some chords sound very strong and final while others can sound weak and unfinished. It is the manipulation of tension and release that allows chord sequences to flow in a natural way. These relationships will become more apparent as you learn more about music
Chords
Chords are specific sets of intervals that are played together to create a very particular harmonic effect. Each chord type has its own specific formula. The numbering system we use to define the intervals in a chord is directly related to the notes in a Major scale. Most chords are built using stacked thirds. You will notice that the major7 chord below uses 3 third intervals in a row.
C D E F G A B (C)
1 2 3 4 5 6 7
1 – 3 – 5 – 7 = Major 7th
We also use flats (b) and sharps (#) in many chord formulas. These simply instruct us to move a given note of the Major scale either up or down a semitone.
C D Eb F G A Bb (C)
1 2 b3 4 5 6 b 7
1 – b3 – 5 – b7 = Minor 7th
Below is a list of common chord types you may come across. Notice that they have been grouped into ‘types’ (Major, Minor, Dominant). We group them together because they share common intervals. You can think of these groups as families as they all share common characteristics.
- Major – the regular or ‘Major’ third is always present
- Minor – the flattened third is always present
- Dominant – the Major third and flat seventh are always present
- Add – the seventh is not present. A 9th,11th or 13th is added onto a triad
- Sus – the third is replaced by either a 2nd or a 4th degree
This is a lot of information to take in so take your time with it and use it as a reference guide when using chords. Try building some of you own using these formulas…
|
MAJOR CHORDS |
MINOR CHORDS |
||
|
Major |
1 3 5 |
Minor |
1 b3 5 |
|
Major 6 |
1 3 5 6 |
Minor 6 |
1 b3 5 6 |
|
Major 6/9 |
1 3 5 6 9 |
Minor 7 |
1 b3 5 b7 |
|
Major 7 |
1 3 5 7 |
Minor 7b5 |
1 b3 b5 b7 |
|
Major 9 |
1 3 5 7 9 |
Minor 9 |
1 b3 5 b7 9 |
|
Major 11 |
1 3 5 7 9 11 |
Minor 11 |
1 b3 5 b7 9 11 |
|
Major 13 |
1 3 5 7 9 11 13 |
Minor 13 |
1 b3 5 b7 9 11 13 |
|
|
|
|
|
|
DOMINANT CHORDS |
ADD CHORDS |
||
|
Dominant 7 |
1 3 5 b7 |
Add9 |
1 3 5 9 |
|
Dominant 9 |
1 3 5 b7 9 |
Add11 |
1 3 5 11 |
|
Dominant 11 |
1 3 5 b7 9 11 |
SUS CHORDS |
|
|
Dominant 13 |
1 3 5 b7 9 11 13 |
Sus2 |
1 2 5 |
|
|
|
Sus4 |
1 4 5 |
|
|
|
|
|
|
DIMINISHED CHORDS |
ALTERED CHORDS |
||
|
Diminished |
1 b3 b5 |
Dominant 7#9 |
1 3 5 b7 #9 |
|
Diminished 7 |
1 b3 b5 bb7 |
Dominant 7b9 |
1 3 5 b7 b9 |
|
AUGMENTED CHORDS |
Dominant 7#5 |
1 3 #5 b7 |
|
|
Augmented |
1 3 #5 |
Dominant 7b5 |
1 3 b5 b7 |
|
Augmented 7 |
1 3 #5 b7 |
|
|
You may be familiar with some uncommon sounding chord names such as Amin9 or G11? Well, these complicated sounding chords are actually quite simple to understand. Simply put, the 9th, 11th and 13th degrees are the 2nd, 4th and 6th degrees up 1 octave. Below we have a Major scale spread across two octaves.

Chords that contain the 9th, 11th or 13th are called “Extended Chords” which relates to the way they extend across two octaves. These chords tend to be used heavily in Jazz and some Blues music. We don’t use the other extended numbers very often (8,10,12 etc) because those notes are already present in triads and seventh chords.
